More than what one player could accumulate even if they had a city on every world and played them all to the max.
Since it's unlikely any player (or players) will ever go to the work of obtaining an acceptable sample size, the confidence provided is a moot point. If anyone ever does, ask me again.
I don’t think you will find many data scientists that agree with you on this. Sample size is one of the most difficult and debated aspects of running experiments. Generally speaking, it‘s not a matter of how small the sample size is, but what you can infer from it. Many experiments/surveys just simply do not have access to unlimited data and so the decision becomes how much precision is provided by what is there. There are several situations outlined in this board already, that warrant a more thorough explanation of why they are wrong, misleading, or accurate.
Marduino makes the claim that he had a sample size of 25, with an expected chance of 10% or more, and 0 successes. This sample size is actually relevant enough, but his/her conclusion is wrong. What their data shows is that we can say with 95% confidence that the RNG’s mean value was between 0 and 13.7%. In other words, there is no proof in this data that the advertised rate is wrong.
Marduino makes the claim that he had a sample size of 57, with an expected chance of 10% or more, and 2 successes. This sample size is also relevant enough, but again his/her conclusion is wrong. Their data shows that we can say with 95% confidence that the RNG’s mean value was between 1% and 12%. Again, no proof in this data that the advertised rate is wrong.
More generally, for the Spring Event there would have been 2 main strategies for pursuing daily prizes: lowest cost of lanterns per % or highest %. The former would have provided about 130 leaps, while the latter closer to 90. Expected value of the first would be about 7.83% and for the second 11.42%, both unsurprisingly providing an expected value of 10 daily prizes. Based on the two sample size options from a single city, winning any value between 5 and 16 of daily prizes would fall within the 95% confidence interval and subsequently would not provide any proof the advertised rate is wrong. Under these conditions, less than 5 or more than 16, would be problematic and worth raising.
In Algona’s diamond experiment, he states a sample size of 10,000, with an expected chance of 1%, and 99 successes. Again, the sample size is relevant is his conclusion is supported. His data shows that we can say with 95% confidence that the WW diamond RNG‘s mean value is between .81% and 1.2%. It does not show that it is 1%, but it shows that 1% is within the confidence interval and there is no proof the advertised rate is wrong. If his results had held at say 5,000 attempts, the 95% confidence interval would be .74% and 1.29%. Halving the sample size again would move the interval to .65% and 1.42%. In none of those cases, can we definitively state that the exact % of the RNG is 1, but there is nothing in the data to suggest it couldn’t be.
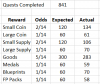
With Pirate’s data, it is much like Algona’s in that it doesn’t definitively answer the question of what % the RNG is running at, but shows that the published rates are within the confidence interval based on the sample provided. If you bundle his data together into 1/14, 2/14, and 5/14 events his data shows:
a.) that the 95% confidence interval for goods is 30.5% to 36.9% encompassing the expected value of 35.7%.
b.) that the 95% confidence interval for small coin/supply is 25.6% to 31.7% encompassing the EV of 28.5%
c.) that the 95% confidence interval for every other outcome is 34.6% to 41.1% encompassing the EV of 35.7%
If either Algona or Pirate had been seeking a more exact value, which I don’t believe was the goal, the only thing that is really of any debate in these two cases is how wide of an interval is sufficient to show the preciseness of that value. That is where the size of the sample would come into discussion as more samples would certainly lead to a smaller width, as demonstrated on the examples above in using 5,000 or 2,500 samples instead of 10,000.
My last example comes from my own experience in the 2020 Forge Bowl. My sample size was 17 throws, with 6 of them resulting in double rewards, something that was only supposed to occur 3% of the time. To be clear, this is not statistically impossible, but it works out that there is about a 1/155,000 chance of this happening, and the 99% confidence interval for the mean RNG for this sample was 13.7% to 65.1%. When we talk about something with such small chances of occurrence, we have to consider the chance that something was not working as intended, even if only temporarily.
In every case above, regardless of sample size, there is something to be learned from the data. The answer isn’t necessarily that someone’s sample size isn’t large enough, rather it’s their interpretation of that sample that is off-base, or in the latter cases that the data supports their assessment.